Unregulated Half wave Power supply

Introduction

This is the first in a series of Power Supply articles I am working on. Each will evolve in complexity, function, and practical application. Before starting power supply experiments, review and follow electrical safety procedures. Here is a short article I wrote on Electrical Safety.

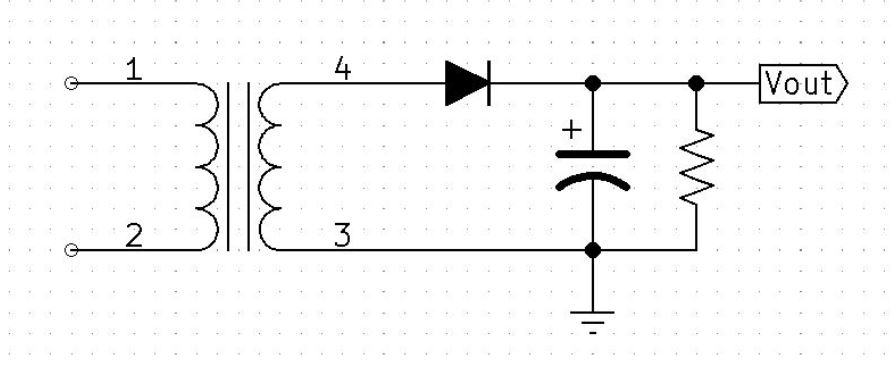
Given

Given: Vpri = 120v 60Hz, Turns ratio = 4:1, C1 = 10uF, RL = 10K Ohms

Calculate Primary Voltage

Start by converting the primary RMS voltage to Peak voltage.

$$Vpeak_{Primary}=\frac{V_{RMS}}{0.707}$$

$$Vpeak_{Primary}=\frac{120V_{RMS}}{0.707}$$

$$Vpeak_{Primary}=169.731vp$$

Primary Voltage Waveform

Calculate Secondary Voltage

Find the Secondary Peak Voltage.

$$Vpeak_{Secondary}=\frac{Vpeak_{Primary}}{turns-ratio}$$

$$Vpeak_{Secondary}=\frac{169.731vp}{4}$$

$$Vpeak_{Secondary}=42.433vp$$

Secondary Voltage Waveform

Find Unfiltered Output Voltage

Imagine the circuit without the filter capacitor. During the positive cycle of the secondary voltage, the diode will be forward-biased and will allow current to flow. During the negative cycle of the secondary voltage, the diode will be reverse biased and no current will flow through the resistor.

$$Vout_{PositiveCycle}=VSecondary_{PositiveCycle}-Vdiode$$

$$Vout_{PositiveCycle}=42.433vp-0.7V$$

$$Vout_{PositiveCycle}=41.733vp$$

$$Vout_{NegativeCycle}=0vp$$

Unfiltered Half-Wave Voltage Waveform

Add Filtering

Calculate what the capacitor discharge voltage will be. When the diode is forward biased, the capacitor will immediately charge to 41.733V (Vsecondary – Vdiode). The capacitor will have one cycle worth of time to discharge, this is a half-wave rectifier, the time will be 1/60hz or 16.667ms. Because we are looking for a discharge voltage, Vfinal will be equal to zero volts in our formula and Vinitial will be equal to 41.733V.

$$VC_{max}=41.733V$$

$$VC_{min}=Vfinal-((Vfinal-Vinitial)e\frac{-time}{RC})$$

$$VC_{min}=0-((0-41.733)e\frac{-16.667mS}{10uFx10K})$$

$$VC_{min}=35.326vp$$

Filtered Output Waveform Voltage

Vrpp & VDC

V ripple peak to peak is found by subtracting Vmax from Vmin & VDC is the average voltage.

$$Vrpp = Vmax-Vmin$$

$$Vrpp= 41.733vp-35.326vp$$

$$Vrpp=6.407vpp$$

$$VDC=\frac{Vmax+Vmin}{2}$$

$$VDC=\frac{41.733V+35.326}{2}$$

$$VDC=38.52V$$

VDC Waveform Voltage represented in blue

Vrms & %ripple

Vrms is the RMS equivalent of the ripple voltage and %ripple is a ratio of Vrms to VDC, describing how well the output DC is filtered.

Notice that the ripple waveform is more triangular than sinusoidal. This is why we use the square root of 3 rather than 2.

$$Vrms=\frac{Vrpp}{2\sqrt{3}}$$

$$Vrms=\frac{6.407}{2\sqrt{3}}$$

$$Vrms=1.85v$$

$$\%ripple=\frac{Vrms}{VDC}\times100$$

$$\%ripple=\frac{1.85}{38.52}\times100$$

$$\%ripple=4.8\%$$