Previous Article in this series
The prerequisite for this article can be read here:
Unregulated Bridge Rectification Pi Filtered Power Supply
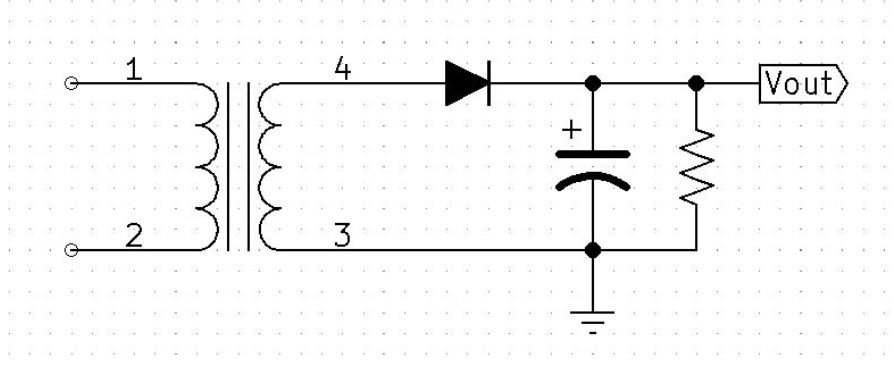
Given
Given: Vpri = 120v 60Hz, Turns ratio = 4:1, C1 = 10uF, RL = 10K Ohms
Review the calculations for this circuit previously covered
Unregulated Halfwave Filtered Power Supply
The problem
The problem with any unregulated power supply is that the DC and ripple voltage will change if the load changes. Our example, with a 10K ohm load, has a DC output voltage of 38.52 volts and a ripple voltage of 6.407vpp. What happens to the DC and ripple voltage if you change the load resistance to 5K ohm or 1K ohm?
Reviewing calculations for VDC and Vrpp with 10K ohm load
$$VC_{max}=41.733V$$
$$VC_{min}=Vfinal-((Vfinal-Vinitial)e\frac{-time}{RC})$$
$$VC_{min}=0-((0-41.733)e\frac{-16.667mS}{10uF \times 10K})$$
$$VC_{min}=35.326vp$$
$$Vrpp = Vmax-Vmin$$
$$Vrpp= 41.733vp-35.326vp$$
$$Vrpp=6.407vpp$$
$$VDC=\frac{Vmax+Vmin}{2}$$
$$VDC=\frac{41.733V+35.326}{2}$$
$$VDC=38.52V$$
Recalculating VDC and Vrpp with a 5K ohm load
$$VC_{max}=41.733V$$
$$VC_{min}=Vfinal-((Vfinal-Vinitial)e\frac{-time}{RC})$$
$$VC_{min}=0-((0-41.733)e\frac{-16.667mS}{10uF \times 5K})$$
$$VC_{min}=29.903vp$$
$$Vrpp = Vmax-Vmin$$
$$Vrpp= 41.733vp-29.903vp$$
$$Vrpp=11.83vpp$$
$$VDC=\frac{Vmax+Vmin}{2}$$
$$VDC=\frac{41.733V+29.903}{2}$$
$$VDC=35.818V$$
Recalculating VDC and Vrpp with a 1K ohm load
$$VC_{max}=41.733V$$
$$VC_{min}=Vfinal-((Vfinal-Vinitial)e\frac{-time}{RC})$$
$$VC_{min}=0-((0-41.733)e\frac{-16.667mS}{10uF \times 1K})$$
$$VC_{min}=7.882vp$$
$$Vrpp = Vmax-Vmin$$
$$Vrpp= 41.733vp-7.882vp$$
$$Vrpp=33.851vpp$$
$$VDC=\frac{Vmax+Vmin}{2}$$
$$VDC=\frac{41.733V+7.882}{2}$$
$$VDC=24.8075V$$