Previous Article in this series
The prerequisite for this article can be read here: Unregulated Fullwave Center-Tapped Filtered Power Supply
Given
Calculate Primary Voltage
Primary Peak to Peak Voltage Waveform
Calculate Secondary Voltage
Find the Secondary Peak Voltage.
Secondary Voltage Waveform
Find Unfiltered Output Voltage
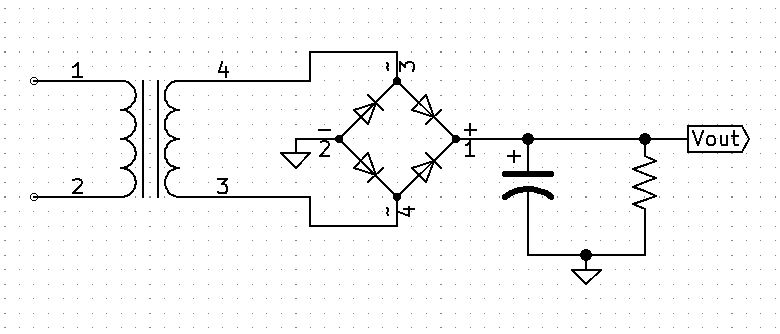
Imagine the circuit without the filter capacitor.
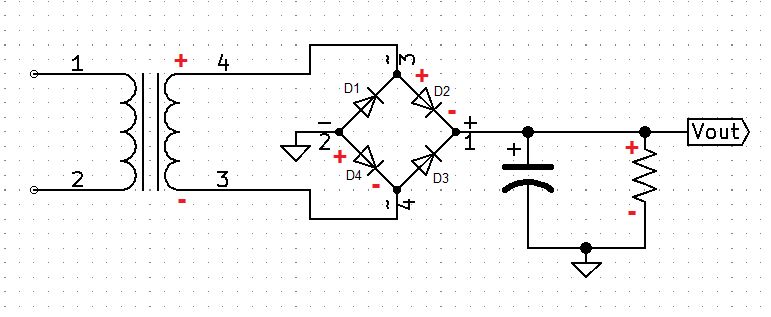
During the positive cycle diodes, D2 and D4 will be forward-biased allowing current to flow to the output.
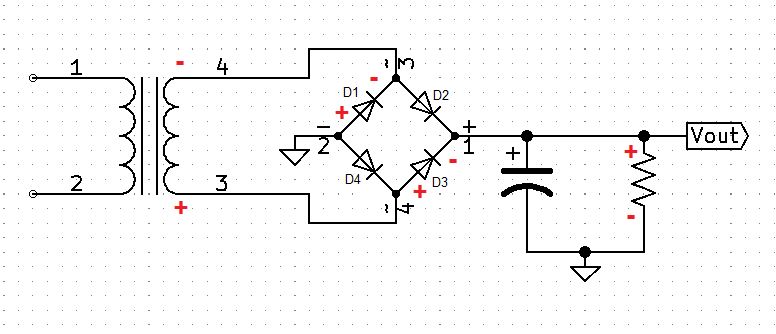
During the negative cycle diodes, D1 and D3 will be forward-biased allowing current to flow to the output.
Unfiltered Output Waveform Voltage 120hz
Add Filtering
Calculate what the capacitor discharge voltage will be. The capacitor will immediately charge to 41.033V (Vsecondary – 2Vdiode). During the valley of the waveform, the capacitor will have one cycle worth of time to discharge, this is a full-wave rectifier, the time will be 1/120hz or8.333ms. Because we are looking for a discharge voltage, Vfinal will be equal to zero volts in our formula and Vinitial will be equal to 41.033V.
$$VC_{max}=41.033V$$
Filtered Output Waveform Voltage 120hz
Vrpp & VDC
V ripple peak to peak is found by subtracting Vmax from Vmin & VDC is the average voltage.
VDC Waveform Voltage represented in blue
Vrms & %ripple
Vrms is the RMS equivalent of the ripple voltage and %ripple is a ratio of Vrms to VDC, describing how well the output DC is filtered.
Notice that the ripple waveform is more triangular than sinusoidal. This is why we use the square root of 3 rather than 2.